3.6.19

3.6.17

3.6.17 En un estudio de dactilografía una característica cuantitativa muy importante es el total de surcos en los 10 dedos del individuo. Supóngase que el total de surcos en los dedos de los individuos en una población tienen distribución aproximadamente normal con una media de 140 y una desviación estándar de 50.

EXAMEN SORPRESA 02/05/2013

EJ. 3.6.5 Y 3.3.7

Ejercicios

Ej. 3.4.5

Ejercico 3.4.4

Examen !!!!!

EJERCICIOS DE DISTRIBUCION BINOMINAL

http://www.vadenumeros.es/sociales/ejemplos-distribucion-binomial.htm

Distribución binomial

la distribucion binomial es una de las distribuciones utillizadas mas ampliamente en estadística aplicada. La distribución se deriva de un procedimiento conocido como ensayo de Bernoulli, nombrando asi en honor,al matemático suizo James  Bernoulli, (11654-1705), quien realizo contribuciones muy importantes en el campo de la probabilidad incluyendo, particularmente, la distribución  binomial. Cuando en un solo ensayo de algún proceso o experimento puede ocurrir solo una de 2 resultados mutuamente excluyentes como vida o muerte alivio o enfermedad, blanco o negro, el ensayo se llama ensayo d Bernoulli.

Una secuencia de ensayos de Bernoulli forma un proceso de ensayo de Bernoulli si se cumple con las siguientes especificaciones:

11 En cada ensayo ocurre uno de dos posibles resultados, mutuamente excluyentes. Uno de los posibles resultados se denota arbitrariamente como exito y/o el otro como un fracaso

22       La probabilidad de un éxito, denotado por  p  permanece constante de un ensayo o  a otro y la probabilidad del fracaso  1- p se denota con la probabilidad  1-p=q

33  los ensayos son independientes, es decir, el resultado de cada ensayo en particular no es afectado por el resultado de cualquier otro ensayo.

L    La probabilidad de obtener exactamente “X” éxitos en “n”  ensayos se escribe como: 

Esta expresión se llama Distribución Binomial.  En la ecuación 3.3.1  F(x)=   se emplea para denotar la probabilidad de “X” éxitos en “n” ensayos.

´¿Cuál es la probabilidad de……

1.       f(x)={3≤X≤5}= 0.32+0.175+0.03802=0.5334

2.       f(x)={1≤X≤3}=0.1378+0.2983+0.32=0.3303

3.       f(x)={X≤3}=0.32+0.175+0.03802=0.5334

4.       f(x)={X≤}=1-0.03802=0.9619

PROBABILIDAD :)

2.7.14 La siguiente tabla muestra 1000 aspirantes a la escuela a de enfermería, clasificadas de acuerdo a las calificaciones obtenidas en el examen de ingreso a la escuela profesional y la calidad del bachillerato de procedencia.

Calidad de la secundaria

	Baja (P)	Promedio (A)	Superior (S)	Total
Bajo(B)	105	60	55	220
Medio(M)	70	175	145	390
Alto(H)	25	65	300	390
Total	200	300	500	1000

 A) Calcular la probabilidad de que un aspirante elegido al azar:

1.       Obtenga una puntuación baja en el examen

2.       Proceda de un bachillerato de alto nivel

3.       Obtenga una calificación alta y proceda de un bachillerato de alto nivel

4.       Que obtenga una calificación baja, dado que proceda de un bachillerato de alto nivel

5.       Haya obtenido una calificación alta o proceda de un bachillerato de alto nivel

 B)      Calcular las siguientes probabilidades

1.       P(A)

2.       P(B)

3.       P(M)

4.       P(A I B)

5.       P(M U P)

6.       P(B I S)  

Ejercicio 2

Ejercicio 2.7.13

En un departamento de salud del estado se recibieron 25 solicitudes de empleo para un puesto de enfermera de sanidad pública. De las solicitantes, diez tienen más de 30 años de edad y quince tienen menos de 30 años. 17 tienen grado de bachiller solamente y 8 tienen grado de maestría. De las que tienen menos de 30 años, 6 tienen grado de maestría. Si se efectúa una elección al azar de entre las 25 solicitantes ¿cuál es la probabilidad de elegir una persona de más de 30 años o con grado de maestría?

	Más de 30 años (A)	Menos de 30 años ( C )	Total
Bachilleres (B)	8	9	17
Maestría (M)	2	6	8
total	10	15	25

Solución

A U M

10+8-2 =16 

Ejercicios

Ejercicio 2.7.11

A cien mujeres casadas se les pregunto qué método de control natal preferían. La siguiente tabla muestra las 100 respuestas de clasificación entrecruzada por nivel de educación.

Método de control natal	Nivel educativo
	Secundaria (A)	Bachillerato (B)	Licenciatura (C)	total
S	15	8	7	30
T	3	7	20	30
V	5	5	15	25
W	10	3	2	15
total	33	23	44	100

Especificar el número de miembros de cada uno de los siguientes conjuntos:

A)     S = 30

B)      Vᴖ C = 15

C)      A= 33

D)     W= 15

E)      V =25

F)      B̅ = 100-23= 77

G)     TᴖB =7

H)     (TᴖC)̅= 100-20=80

Probabilidad Condicionada

Probabilidad Condicionada Ejercicios

Probabilidad

Probabilidad

Ejercicios

Resuelve los sigueintes ejercicios. Cuando termines, oprime el botón "Evalua". Buena suerte!!.

1. Si tiro un dado:
   ¿Cuál es la probabilidad de obtener un número par?     3/4 1/2 2/4 1/4
   
   ¿Cuál es la probabilidad de obtener un número mayor de 2?     3/4 2/3 2/4 1/4
   
2. En un salón de clases hay 30 alumnos de los cuales 10 son niñas y 20 niños ¿Cuál es la probabilidad de que al elegir un estudiante éste sea niña?
       3/4 1/3 2/4 1/4
   
3. En una población de 2000 habitantes, 80 padecen afecciones cardiacas ¿Cuál es la probabilidad de emplear a alguien proveniente de este lugar, que no esté enfermo?
   
       12/24 11/32 24/25 11/41
   
4. En una urna hay 10 bolas de colores. 2 son rojas, 4 azules y 4 amarillas.
   a) ¿Cuál es la probabilidad de que al escoger una al azar ésta sea roja?     1/4 1/2 1/5 3/5
   
   b) Si yo sacó de la urna una bola azul y una roja. ¿Cuál es la probabilidad de que al sacar una bola ésta sea azul?
   
       3/8 1/3 2/5 1/4
   
5. En una colonia se entrevistaron a 50 familias, 10 dijeron transportarse en coche propio a sus trabajos y 30 dijeron utilizar algún transporte público. ¿Cuál es la probabilidad de que al seleccionar una familia de esa colonia utilice el transporte público?
       1/4 1/2 1/5 3/5

Probabilidad

Cálculo de la Probabilidad

Para calcular la probabilidad de un evento se toma en cuenta todos los casos posibles de ocurrencia del evento; es decir, de cuántas formas puede ocurrir determinada situación. 

Los casos favorables de ocurrencia de un evento serán los que cumplan con la condición que estoy buscando. 

Así para el tiro de una moneda tengo 2 casos posibles de ocurrencia (o cae águila o cae sol) y sólo 1 caso favorable de que pueda caer águila (pues sólo hay un águila en la moneda). 

Para calcular la probabilidad de un evento se utiliza la siguiente fórmula: 

 

Para nuestro ejemplo: Probabilidad de "que caiga un águila" tenemos: 

 
 

Por lo tanto, existe una probabilidad del 50% que yo obtenga un águila al tirar una moneda. 

Veamos otro ejemplo: Si yo tengo una canasta llena de peras y manzanas, de las cuales hay 20 peras y 10 manzanas. ¿Qué fruta es más probable que saque al azar de la canasta? 

Para este ejemplo tenemos que 30 es el total de frutas en la canasta; es decir los casos posibles. Para calcular la probabilidad de sacar una manzana mis casos favorables son 10 puesto que existen sólo 10 manzanas. Así, aplicando la fórmula obtenemos que: 

ó 33.3% probable 

Calculando igual, la probabilidad de sacar pera es: 

 ó 66.7% probable 

Como 66.7 es mayor que 33.3 es más probable que saque una pera, pues hay más peras que manzanas en la canasta. 

Fíjate bien que 33.3% + 66.7% es igual al 100% porque siempre que saques algo de la canasta es seguro que saques una fruta. 

Así, el valor de la probabilidad de un evento imposible es 0 mientras que la probabilidad de un evento seguro es 1; porque: 

     

Probabilidad de un evento

COMBINACIÓN Y PERMUTACIÓN

Combinaciones y permutaciones

¿Qué diferencia hay?

Normalmente usamos la palabra "combinación" descuidadamente, sin pensar en si el orden de las cosas es importante. En otras palabras:

	"Mi ensalada de frutas es una combinación de manzanas, uvas y bananas": no importa en qué orden pusimos las frutas, podría ser "bananas, uvas y manzanas" o "uvas, manzanas y bananas", es la misma ensalada.
	"La combinación de la cerradura es 472": ahora sí importa el orden. "724" no funcionaría, ni "247". Tiene que ser exactamente 4-7-2.

Así que en matemáticas usamos un lenguaje más preciso:

	Si el orden no importa, es una combinación.
	Si el orden sí importa es una permutación.

Permutaciones

Hay dos tipos de permutaciones:

1. Se permite repetir: como la cerradura de arriba, podría ser "333".
2. Sin repetición: por ejemplo los tres primeros en una carrera. No puedes quedar primero y segundo a la vez.

1. Permutaciones con repetición

Son las más fáciles de calcular. Si tienes n cosas para elegir y eliges r de ellas, las permutaciones posibles son:

n × n × ... (r veces) = n^r

(Porque hay n posibilidades para la primera elección, DESPUÉS hay n posibilidades para la segunda elección, y así.)

Por ejemplo en la cerradura de arriba, hay 10 números para elegir (0,1,...,9) y eliges 3 de ellos:

10 × 10 × ... (3 veces) = 10³ = 1000 permutaciones

Así que la fórmula es simplemente:

nr

donde n es el número de cosas que puedes elegir, y eliges r de ellas (Se puede repetir, el orden importa)

2. Permutaciones sin repetición

En este caso, se reduce el número de opciones en cada paso.

Por ejemplo, ¿cómo podrías ordenar 16 bolas de billar? Después de elegir por ejemplo la "14" no puedes elegirla otra vez.

Así que tu primera elección tiene 16 posibilidades, y tu siguiente elección tiene 15 posibilidades, después 14, 13, etc. Y el total de permutaciones sería:

16 × 15 × 14 × 13 ... = 20,922,789,888,000

Pero a lo mejor no quieres elegirlas todas, sólo 3 de ellas, así que sería solamente:

16 × 15 × 14 = 3360

Es decir, hay 3,360 maneras diferentes de elegir 3 bolas de billar de entre 16.

¿Pero cómo lo escribimos matemáticamente? Respuesta: usamos la "función factorial"

	La función factorial (símbolo: !) significa que se multiplican números descendentes. Ejemplos: 4! = 4 × 3 × 2 × 1 = 24 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040 1! = 1
Nota: en general se está de acuerdo en que 0! = 1. Puede que parezca curioso que no multiplicar ningún número dé 1, pero ayuda a simplificar muchas ecuaciones.

Combinaciones

También hay dos tipos de combinaciones (recuerda que ahora el orden no importa):

1. Se puede repetir: como monedas en tu bolsillo (5,5,5,10,10)
2. Sin repetición: como números de lotería (2,14,15,27,30,33)

1. Combinaciones con repetición

En realidad son las más difíciles de explicar, así que las dejamos para luego.

2. Combinaciones sin repetición

Así funciona la lotería. Los números se eligen de uno en uno, y si tienes los números de la suerte (da igual el orden) ¡entonces has ganado!

La manera más fácil de explicarlo es:

• imaginemos que el orden sí importa (permutaciones),
• después lo cambiamos para que el orden no importe.

Volviendo a las bolas de billar, digamos que queremos saber qué 3 bolas se eligieron, no el orden.

Ya sabemos que 3 de 16 dan 3360 permutaciones.

Pero muchas de ellas son iguales para nosotros, porque no nos importa el orden.

Por ejemplo, digamos que se tomaron las bolas 1, 2 y 3. Las posibilidades son:

El orden importa	El orden no importa
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1	1 2 3

Así que las permutaciones son 6 veces más posibilidades.

De hecho hay una manera fácil de saber de cuántas maneras "1 2 3" se pueden ordenar, y ya la sabemos. La respuesta es:

3! = 3 × 2 × 1 = 6

(Otro ejemplo: 4 cosas se pueden ordenar de 4! = 4 × 3 × 2 × 1 = 24 maneras distintas, ¡prueba tú mismo!)

Así que sólo tenemos que ajustar nuestra fórmula de permutaciones para reducir por las maneras de ordenar los objetos elegidos (porque no nos interesa ordenarlos):

Esta fórmula es tan importante que normalmente se la escribe con grandes paréntesis, así:

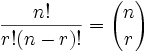donde n es el número de cosas que puedes elegir, y eliges r de ellas (No se puede repetir, el orden no importa)

Y se la llama "coeficiente binomial".

NÚMERO FACTORIAL

COMBINACIÓN Y PERMUTACIÓN.

Factorial

DADO UN NUMERO ENTERO POSITIVO n  EL PRODUCTO DE TODOS LOS ENTEROS POSITIVOS DESDE n HASTA  1 SE LLAMA n FACTORIAL

EJERCICIO 2.5.7

₄C₃= 4!/ 3! * 2!  = 4

EJERCICIO 2.5.8

₄C₂^{= 4! * 3! /1! * 2! = 6}

EJERCICIO 2.5.9

₈C₃*₈C₃*₈C₂=8!/ 5! * 3!* 8!/ 5! * 3! *8!/ 6! * 6!   = 8*7*6*5*4*3*2*1/ 5! 3*2*1 * 8*7*6 /3*2*1 * 8*7*6*5*4*3*2*1/ 6! *2*1

= (56)(56)(28) =   87808

EJERCICIO 2.5.10

_1OP₃ = 10! / (10-3)! = 10!/7! =10*9*8*7*6*5*4*3*2*1 / 7*6*5*4*3*2*1

=720

Clase 14 de febrero 2013

DESVIACIÓN ESTANDAR

Desviación estándar

Clase	Marca de clase	Frecuencia	Mi- X	(Mi-X)2	(Mi-X)2 fi
10-19	14.5	5	-22.1	488.41	2442.05
20-29	24.5	19	-12.1	146.41	2781.79
30-39	34.5	10	-2.1	4.41	44.1
40-49	44.5	13	7.9	62.41	811.33
50-59	54.5	4	17.9	320.41	1281.64
60-69	64.5	4	27.9	778.41	3113.64
70-79	74.5	2	37.9	1436.41	2872.82

Total= 13347.37

·         Varianza

13347.37/56= 238.5459

·         Desviación estándar

                                                           

 raíz cuadrada de 238.5459    =15.44